How to make hexagons: Difference between revisions
-u ndefined- (talk | contribs) (Adapted from old article by LukaszM) |
-u ndefined- (talk | contribs) m (Rename images and add link) |
||
| Line 5: | Line 5: | ||
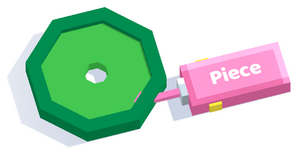
Hexagons are made out of 6 square pieces, properly placed, and rotated. First of all, we need to create a square piece. We're going to create a green hexagon with a darker boundary, so our piece looks like this: | Hexagons are made out of 6 square pieces, properly placed, and rotated. First of all, we need to create a square piece. We're going to create a green hexagon with a darker boundary, so our piece looks like this: | ||
{{Image|Hexagon piece.png}} | |||
This piece will be copied 5 times and the other pieces will be placed relative to the original one. To obtain the coordinates of the remaining pieces, we need to add the following [[vector]]s to the position of the original piece: | This piece will be copied 5 times and the other pieces will be placed relative to the original one. To obtain the coordinates of the remaining pieces, we need to add the following [[vector]]s to the position of the original piece: | ||
* (-0.317, 0, 0.183), | * <code>(-0.317, 0, 0.183)</code>, | ||
* (-0.317, 0, 0.549), | * <code>(-0.317, 0, 0.549)</code>, | ||
* (0, 0, 0.732), | * <code>(0, 0, 0.732)</code>, | ||
* (0.317, 0, 0.183), | * <code>(0.317, 0, 0.183)</code>, | ||
* (0.317, 0, 0.549). | * <code>(0.317, 0, 0.549)</code>. | ||
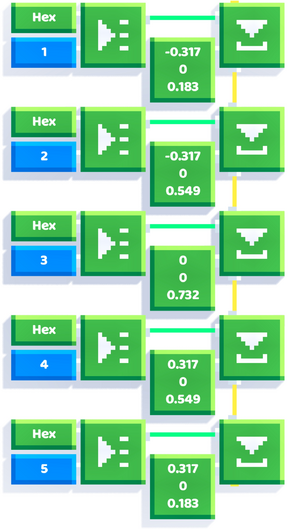
These coordinates are not exact (the exact coordinates are irrational and they require a square root of three), but three decimal places is enough for our hexagon to look good. Let's put them in a list (starting from index 1 for convenience): | These coordinates are not exact (the exact coordinates are irrational and they require a square root of three), but three decimal places is enough for our hexagon to look good. Let's put them in a [[list]] (starting from index 1 for convenience): | ||
{{Image|Hexagon positions.png}} | |||
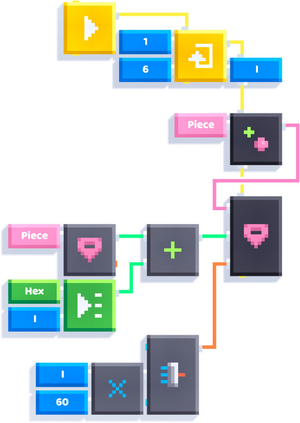
Now our hexagon can be created with a simple [[loop]]. We create the remaining pieces and we set their positions using the list above. We also need to rotate them (by 60°, 120° etc) and for that, we're going to use the [[Make Rotation]] block. The loop looks like this: | Now our hexagon can be created with a simple [[loop]]. We create the remaining pieces and we set their positions using the list above. We also need to rotate them (by 60°, 120° etc.) and for that, we're going to use the [[Make Rotation]] block. The loop looks like this: | ||
{{Image|Hexagon script.png}} | |||
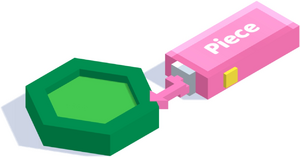
Let's start the script now. See what happened to our original object! | Let's start the script now. See what happened to our original object! | ||
{{Image|Hexagon hexagon.png}} | |||
Here we go! A perfect regular hexagon! | Here we go! A perfect regular hexagon! | ||
| Line 41: | Line 41: | ||
This is how it looks in Fancade. Here we use the fact that cotangent of an angle is equal to its [[Cos|cosine]] divided by its [[Sin|sine]]: | This is how it looks in Fancade. Here we use the fact that cotangent of an angle is equal to its [[Cos|cosine]] divided by its [[Sin|sine]]: | ||
{{Image|Hexagon advanced calculate offset.png}} | |||
Now, to calculate the positions of the remaining pieces, we can subtract '''A''' from the position of the original object and then add '''A''' rotated by a certain angle. Here's how it looks: | Now, to calculate the positions of the remaining pieces, we can subtract '''A''' from the position of the original object and then add '''A''' rotated by a certain angle. Here's how it looks: | ||
{{Image|Hexagon advanced calculate position.png}} | |||
For '''N''' = 6 and '''X''' = '''Z''' = 1, we obtain the exact same hexagon as in the classic method, without using any additional lists! After changing the value of '''N''', we can obtain different polygons, for instance a pentagon: | For '''N''' = 6 and '''X''' = '''Z''' = 1, we obtain the exact same hexagon as in the classic method, without using any additional lists! After changing the value of '''N''', we can obtain different polygons, for instance a pentagon: | ||
{{Image|Hexagon advanced 5 sides.png}} | |||
If '''N''' is bigger than 6, we obtain a polygon with a hole in the middle. To avoid that, we simply need to enlarge our original object and change the values of '''X''' and '''Z'''. | If '''N''' is bigger than 6, we obtain a polygon with a hole in the middle. To avoid that, we simply need to enlarge our original object and change the values of '''X''' and '''Z'''. | ||
{{Image|Hexagon advanced 8 sides.png}} | |||
[[Category:Scripting]] | [[Category:Scripting]] | ||
Latest revision as of 12:45, 21 June 2025
This is a tutorial on how to create a perfect regular hexagon in Fancade. This exact method is used to create hexagons in games Hexalink, Hexoban, and Hexals.
Classic method
Hexagons are made out of 6 square pieces, properly placed, and rotated. First of all, we need to create a square piece. We're going to create a green hexagon with a darker boundary, so our piece looks like this:

This piece will be copied 5 times and the other pieces will be placed relative to the original one. To obtain the coordinates of the remaining pieces, we need to add the following vectors to the position of the original piece:
(-0.317, 0, 0.183),(-0.317, 0, 0.549),(0, 0, 0.732),(0.317, 0, 0.183),(0.317, 0, 0.549).
These coordinates are not exact (the exact coordinates are irrational and they require a square root of three), but three decimal places is enough for our hexagon to look good. Let's put them in a list (starting from index 1 for convenience):
Now our hexagon can be created with a simple loop. We create the remaining pieces and we set their positions using the list above. We also need to rotate them (by 60°, 120° etc.) and for that, we're going to use the Make Rotation block. The loop looks like this:
Let's start the script now. See what happened to our original object!
Here we go! A perfect regular hexagon!
Advanced method
Instead of creating the list of positions, they can be calculated in Fancade using trigonometric functions. Using this method, we can also create regular polygons with different number of sides!
We need three additional variables. Variable N is the number of sides of our polygon, while X and Z denote the size of our original square object.
Now we need to calculate the vector from the origin of our polygon to the origin of our square object. We're going to call it A. Its X and Y coordinates are both equal to 0, while the Z coordinate can be computed using trigonometry:
- A = (0, 0, 0.5(Z - X ⋅ cot(180°/N))).
This is how it looks in Fancade. Here we use the fact that cotangent of an angle is equal to its cosine divided by its sine:
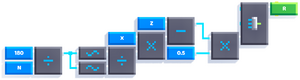
Now, to calculate the positions of the remaining pieces, we can subtract A from the position of the original object and then add A rotated by a certain angle. Here's how it looks:
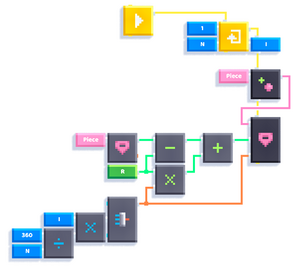
For N = 6 and X = Z = 1, we obtain the exact same hexagon as in the classic method, without using any additional lists! After changing the value of N, we can obtain different polygons, for instance a pentagon:

If N is bigger than 6, we obtain a polygon with a hole in the middle. To avoid that, we simply need to enlarge our original object and change the values of X and Z.