Cross Product: Difference between revisions
Nikitaivanov (talk | contribs) (Created page with "The Cross Product calculates the cross product of the two input vectors, and outputs another vector. /uploads/Cross Product1.png == Details == The Cross Product is a way of multiplying two vectors together. We can calculate the Cross Product of two vectors this way, let's say that the cross product of A and B is vector C: Cx = Ay × Bx - Az × By\ Cy = Az × Bx - Ax × Bz\ Cz = Ax × By - Ay × Bx It outputs the vector that is perp...") |
(Updated and revisited the page) |
||
| Line 1: | Line 1: | ||
{{Block | |||
|image=Cross Product.png | |||
|type=s | |||
|folder=math | |||
|input1={{Port|v}} | |||
|input2={{Port|v}} | |||
|output1={{Port|v|Cross Product}} | |||
}} | |||
Calculates the [https://en.wikipedia.org/wiki/Cross_product cross product] of the two input vectors. | |||
== Details == | == Details == | ||
The Cross Product is a way of multiplying two vectors together. | The Cross Product is a way of multiplying two vectors together. | ||
We can calculate the Cross Product of two vectors this way, let's say that the cross product of A and B is vector C: | We can calculate the Cross Product of two vectors this way, let's say that the cross product of A and B is vector C: | ||
Cx = Ay × Bx - Az × By | <code> | ||
Cy = Az × Bx - Ax × Bz | Cx = Ay × Bx - Az × By | ||
Cy = Az × Bx - Ax × Bz | |||
Cz = Ax × By - Ay × Bx | Cz = Ax × By - Ay × Bx | ||
</code> | |||
It outputs the vector that is perpendicular to both input vectors (or the plane spanned by those | It outputs the vector that is perpendicular to both input vectors (or the plane spanned by those vectors). | ||
[[File: | [[File:Crossprod.png|frame|right]] | ||
The length of | The length of the output vector is equal to the area of the parallelogram formed by the input vectors (each vector gives a pair of parallel sides). | ||
[[Category:Blocks]] | [[Category:Blocks]] | ||
Latest revision as of 15:05, 17 May 2024
Cross Product
| Type | Script block |
| Collider | None |
| Folder | Math |
| Ports | |
|---|---|
| Inputs | Vector Vector |
| Outputs | Cross Product |
Calculates the cross product of the two input vectors.
Details
The Cross Product is a way of multiplying two vectors together. We can calculate the Cross Product of two vectors this way, let's say that the cross product of A and B is vector C:
Cx = Ay × Bx - Az × By
Cy = Az × Bx - Ax × Bz
Cz = Ax × By - Ay × Bx
It outputs the vector that is perpendicular to both input vectors (or the plane spanned by those vectors).
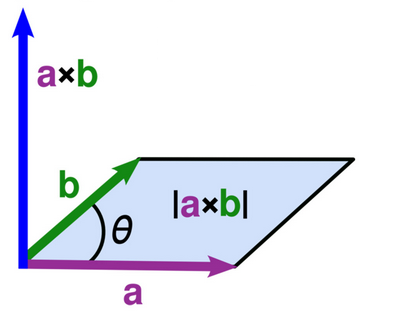
The length of the output vector is equal to the area of the parallelogram formed by the input vectors (each vector gives a pair of parallel sides).
